A Star Algorithm
In preparation for constructing the final leg of the robot, I opted to first simulate it in a digital environment. This approach offers significant advantages, including reduced costs and the ability to test various inputs without the risk of damaging the actual leg. The primary goal of this simulator is to develop a movement path for the leg in a two-dimensional space.
It's important to note that this simulation does not attempt to replicate real-world conditions. Instead, it focuses on pathfinding, allowing me to adjust specific features of the leg, such as the lengths of the leg segments, the width of the step, and the height. Further details on these adjustments will be discussed later.
What is the A* Algorithm and Why Use It?
The main motivation behind using the A* algorithm is to efficiently find the shortest path between a starting point and an ending point while navigating around obstacles. Here’s a detailed breakdown of how the A* algorithm works:
-
Grid Creation: The first step is to create a 2D grid, dividing our simulation window into multiple squares or rectangles. This grid will serve as the framework for pathfinding.
-
Set Start and Goal Points: We designate a starting point, known as the source cell, and an ending point, referred to as the goal cell.
-
Parameters: The A* search algorithm utilizes two key parameters: 'g' and 'h'.
- g: This represents the movement cost from the starting point to a given square on the grid.
- h: This is the heuristic estimate of the movement cost from the given square to the goal cell.
-
Pathfinding: To determine the optimal path, we calculate the sum of 'g' and 'h' for each square. The square with the lowest combined cost (denoted as 'f') is chosen as part of the path. The algorithm continues this process, comparing potential paths and selecting the one with the lowest 'f' value.
There are several heuristic methods available to estimate the shortest path. For my simulation, I have chosen the Euclidean Distance heuristic, which allows for diagonal movement between grid squares. If you are interested in exploring other heuristic options, I recommend reviewing the sources listed at the end of this article.
The final step in the A* algorithm is to compare the total costs (f values) of potential paths. For simplicity, let’s consider two potential cells:
- Cell 1 estimated values: \(f_1 = g_1 + h_1\)
- Cell 2 estimated values: \(f_2 = g_2 + h_2\)
If \(f_1<f_2\), the algorithm selects Cell 1 as the next move, in this case to the right within the same row. Although the algorithm evaluates all cells around the source cell, but I simplify the example by focusing on just two cells.
After selecting the next cell, the algorithm repeats the process, continuing until the goal cell is reached. While this may seem overly complex for simulating leg movement, A* provides significant advantages for future implementations. It can account for obstacles, ensure unreachable points are avoided, and model the foot’s movement path more naturally.
Using A* prepares the simulation for more advanced scenarios, making it a robust choice for developing realistic and efficient movement paths.
Pygame
For the display environment, I will use Pygame, a library commonly used for designing games or simple human-machine interfaces (HMI). Pygame is perfectly suited for my needs, as the simulation will not be overly complex. It will serve to visualize the movement of each part of the robot leg.
One of the challenges with Pygame is that the coordinate system starts at the top-left corner of the window (0,0). This means that when calculating hinge points, you need to adjust your calculations accordingly. Our goal is to split the entire window into grids. In the code, you will be able to change the width and height of the displayed window and consequently also change the parameters of the squares (which can become rectangles if the number of columns and rows isn't the same, but it's also okay). What's' more, you can edit the length of the thigh and the calf of the leg to get different results.
To display a line or part of the leg in Pygame, you need to know the starting and ending coordinates of that line. These coordinates will be calculated for each frame of the movement using inverse kinematics. For those interested in a deeper understanding of inverse kinematics, I invite you to read the first chapter of my series on building a robot dog, available on my blog: Robot Leg Theory.
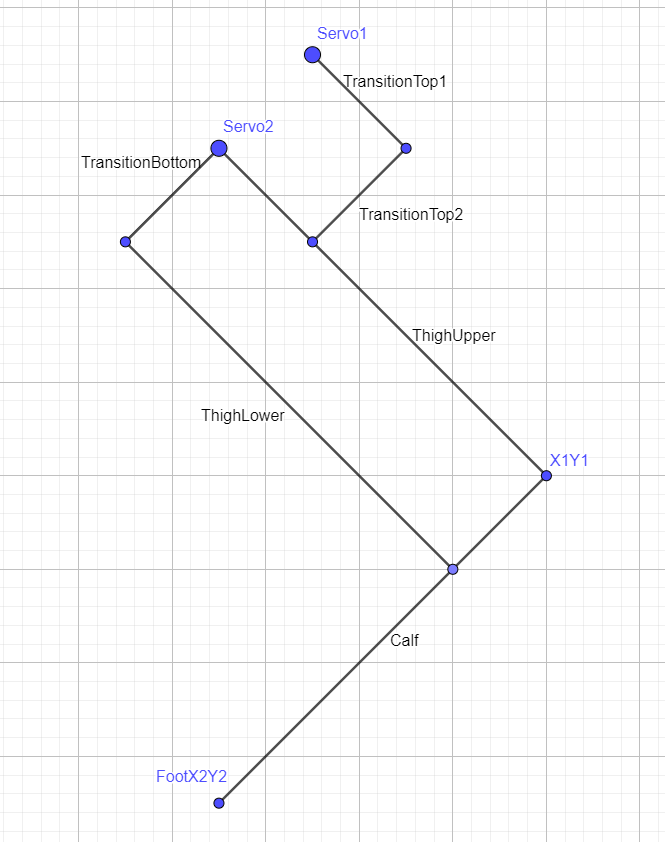
Below is a preview of the final skeletal structure of the leg:
Code explanation
Parameters of the leg for tunning:
# Window size
WIDTH = 600
HEIGHT = 600
# Lengths of leg parts:
a1 = 200
a2 = 200
Robot:
Sets the robot's current position.
def set(self, mx, my):
self.mx = mx
self.my = my
Analyzes data by calculating positions for different angles q1 and q2, including limits of the movement.
def data_analyzing(self, screen, q1_lims=[-3, -1.55], q2_lims=[1, 1.85], N=5):
q1_s = np.linspace(q1_lims[0], q1_lims[1], N)
q2_s = np.linspace(q2_lims[0], q2_lims[1], N)
for q1 in q1_s:
x_1 = np.cos(q1) * a1
y_1 = np.sin(q1) * a1
for q2 in q2_s:
x_2 = np.cos(q2) * a1 + x_1
y_2 = np.sin(q2) * a1 + y_1
pygame.draw.circle(screen, blue, (x_2, y_2), 3, width=3)
self.x_data.append(np.abs(x_2))
self.y_data.append(np.abs(y_2))
self.q1_data.append(round((0.5 * np.pi + q1) * -180 / np.pi, 1))
self.q2_data.append(round((-0.5 * np.pi + q1 + q2) * -180 / np.pi, 1))
Uses A* search algorithm to find paths to multiple destinations on a grid. Defines a grid, cell dimensions, source, and destination list. If you want to change desired path of the foot(the furthest or highest point, change dest_list and src. If you want to add obstacles, change in grid from 0 to 1)
grid = [
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
]
cell_width = WIDTH/len(grid)
cell_height = HEIGHT/len(grid[0])
src = [8, 6]
dest_list = ([5, 4], [8, 3], [8, 7])
For each destination in dest_list. Creates an AStarSearch object and performs the search. Traces the path found by A* and stores the path points in self.path_points.
print(f"Searching path to destination: {dest}")
a_star = AStarSearch(grid, src, dest)
a_star.a_star_search()
path = a_star.trace_path()
src = dest
for i in path:
vertical = cell_width * (i[1]-.5)
horizontal = cell_height * (i[0]-.5)
print(f'vertical: {vertical}; horizontal: {horizontal}')
self.path_points.append((vertical, horizontal)) # Collect path points
Initialize the calculations of coordniates for the found path and update the position of the foot.
robot.movement()
if self.path_points:
self.mx, self.my = self.path_points.pop(0) # Update position to the next path point
For better understanding of the construction.
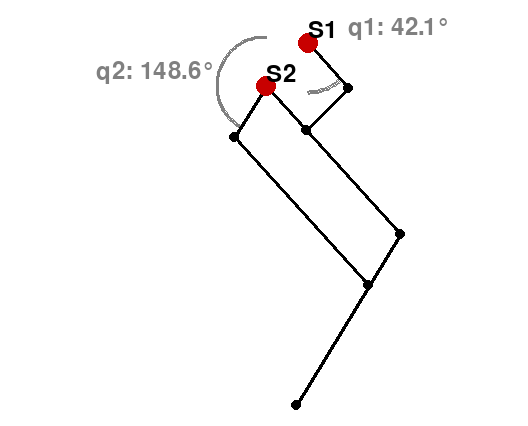
Calculate the inverse kinematic of given x2 and y2 coordinates, which are the points of foot and the outcome is angle of the top 'servos' and points of joint in the knee.
C = ((WIDTH/2 - self.mx)**2 + (.15 * HEIGHT - self.my)**2 - a1**2 - a2**2) / (2 * a1 * a2)
font = pygame.font.Font(None, 36)
if -1 <= C <= 1: # Only calculate q1 and q2 if the target is reachable
# Inverse Kinematics
q2 = np.arccos(C)
q1 = np.arctan2((.15 * HEIGHT - self.my), (WIDTH / 2 - self.mx)) - np.arctan2(a2 * np.sin(q2), a1 + a2 * np.cos(q2))
self.y = a1 * np.sin(q1)
self.x = a1 * np.cos(q1)
self.y2 = a2 * np.sin(q2) + self.y
self.x2 = a2 * np.cos(q2) + self.x
From the calculated values of q1, q2, x1, x2, y1, y2, and width/height, we can calculate the coordinates of the starting and ending points of the parts in the window (including the (0,0) coordinate in the top-left corner).
# Drawing pieslice for angles
pygame.draw.arc(screen, grey, (WIDTH / 2 + .30 * a1 * np.sqrt(2) / 2 - 50, .15 * HEIGHT - .30 * a1 * np.sqrt(2) / 2 - 50, 100, 100), 1.5 * np.pi, np.pi - q1, 2)
textq1 = font.render(f'q1: {round((0.5 * np.pi + q1) * -180 / np.pi, 1)}°', True, grey)
screen.blit(textq1, (WIDTH / 2 + .30 * a1 * np.sqrt(2) / 2 + 40, .15 * HEIGHT - .48 * a1 * np.sqrt(2) / 2 - 3))
pygame.draw.arc(screen, grey, (WIDTH / 2 - 50, .15 * HEIGHT - 50, 100, 100), .5 * np.pi, np.pi - (q1 + q2), 3)
textq2 = font.render(f'q2: {round((-0.5 * np.pi + q1 + q2) * -180 / np.pi, 1)}°', True, grey)
screen.blit(textq2, (WIDTH / 2 - 170, HEIGHT * 0.11 - 3))
# text = font.render("Target is reachable!", True, black)
# Thigh upper
pygame.draw.line(screen, black, (WIDTH / 2, HEIGHT * 0.15), (WIDTH / 2 - self.x, .15 * HEIGHT - self.y), 4)
# Calf
pygame.draw.line(screen, black, (WIDTH / 2 - self.x, .15 * HEIGHT - self.y), (self.mx, self.my), 4)
# Transition top1
pygame.draw.line(screen, black, (WIDTH / 2 + .30 * a1 * np.sqrt(2) / 2, .15 * HEIGHT - .30 * a1 * np.sqrt(2) / 2), (WIDTH / 2 + .30 * a1 * (np.sqrt(2) / 2 - np.cos(q1)), .15 * HEIGHT - .30 * a1 * (np.sqrt(2) / 2 + np.sin(q1))), 4)
# Transition top2
pygame.draw.line(screen, black, (WIDTH / 2 + .30 * a1 * (np.sqrt(2) / 2 - np.cos(q1)), .15 * HEIGHT - .30 * a1 * (np.sqrt(2) / 2 + np.sin(q1))), ((WIDTH / 2 - self.x * .30), .15 * HEIGHT - self.y * .30), 4)
# Transition bottom
pygame.draw.line(screen, black, (WIDTH / 2, HEIGHT * 0.15), (WIDTH / 2 - .30 * a1 * np.cos(q1 + q2), HEIGHT * 0.15 - .30 * a1 * np.sin(q1 + q2)), 4)
# Thigh lower
pygame.draw.line(screen, black, (WIDTH / 2 - .30 * a1 * np.cos(q1 + q2), HEIGHT * 0.15 - .30 * a1 * np.sin(q1 + q2)), (.7 * (WIDTH / 2 - self.x) + .30 * self.mx, .7 * (.15 * HEIGHT - self.y) + .30 * self.my), 4)
# Servo 1
pygame.draw.circle(screen, red, (WIDTH / 2 + .30 * a1 * np.sqrt(2) / 2, .15 * HEIGHT - .30 * a1 * np.sqrt(2) / 2), 10, width=10)
# Servo 2
pygame.draw.circle(screen, red, (WIDTH / 2, HEIGHT * 0.15), 10, width=10)
# Aesthetic thing
pygame.draw.circle(screen, black, (WIDTH / 2 - self.x, .15 * HEIGHT - self.y), 5, width=5)
pygame.draw.circle(screen, black, (self.mx, self.my), 5, width=5)
pygame.draw.circle(screen, black, (WIDTH / 2 + .30 * a1 * (np.sqrt(2) / 2 - np.cos(q1)), .15 * HEIGHT - .30 * a1 * (np.sqrt(2) / 2 + np.sin(q1))), 5, width=5)
pygame.draw.circle(screen, black, ((WIDTH / 2 - self.x * .30), .15 * HEIGHT - self.y * .30), 5, width=5)
pygame.draw.circle(screen, black, (WIDTH / 2 - .30 * a1 * np.cos(q1 + q2), HEIGHT * 0.15 - .30 * a1 * np.sin(q1 + q2)), 5, width=5)
pygame.draw.circle(screen, black, (.7 * (WIDTH / 2 - self.x) + .30 * self.mx, .7 * (.15 * HEIGHT - self.y) + .30 * self.my), 5, width=5)
s1name = font.render("S1", True, black)
screen.blit(s1name, (WIDTH / 2 + .30 * a1 * np.sqrt(2) / 2, .15 * HEIGHT - .48 * a1 * np.sqrt(2) / 2))
s2name = font.render("S2", True, black)
screen.blit(s2name, (WIDTH / 2, HEIGHT * 0.11))
AStarSearch:
Validates the source and destination cells.
def is_valid(self, row, col):
return (row >= 0) and (row < self.ROW) and (col >= 0) and (col < self.COL)
Checks if the source or destination is blocked.
def is_unblocked(self, row, col):
return self.grid[row][col] == 0
Checks if the source is the destination.
def is_destination(self, row, col):
return row == self.dest[0] and col == self.dest[1]
Calculates the heuristic value using the Euclidean distance to the destination.
def calculate_h_value(self, row, col):
return ((row - self.dest[0]) ** 2 + (col - self.dest[1]) ** 2) ** 0.5
Traces back from the destination to the source using parent pointers to reconstruct the path.
def trace_path(self):
path = []
row = self.dest[0]
col = self.dest[1]
while not (self.cell_details[row][col].parent_i == row and self.cell_details[row][col].parent_j == col):
path.append((row, col))
temp_row = self.cell_details[row][col].parent_i
temp_col = self.cell_details[row][col].parent_j
row = temp_row
col = temp_col
path.append((row, col))
path.reverse()
return path
Creates the closed_list to track visited cells.
closed_list = [[False for _ in range(self.COL)] for _ in range(self.ROW)]
Initializes the start cell in cell_details and pushes it onto the open_list (priority queue).
i, j = self.src
self.cell_details[i][j].f = 0
self.cell_details[i][j].g = 0
self.cell_details[i][j].h = 0
self.cell_details[i][j].parent_i = i
self.cell_details[i][j].parent_j = j
open_list = []
heapq.heappush(open_list, (0.0, i, j))
found_dest = False
Pops the cell with the lowest f value from the open_list and marks the current cell as visited in the closed_list.
p = heapq.heappop(open_list)
i, j = p[1], p[2]
closed_list[i][j] = True
Iterates through all possible movements (8 directions, including diagonals).
directions = [(0, 1), (0, -1), (1, 0), (-1, 0), (1, 1), (1, -1), (-1, 1), (-1, -1)]
for dir in directions:
new_i, new_j = i + dir[0], j + dir[1]
For each direction:
Validates the new cell and checks if the new cell is the destination. If it is, sets the parent pointers and traces the path.
if self.is_valid(new_i, new_j) and self.is_unblocked(new_i, new_j) and not closed_list[new_i][new_j]:
if self.is_destination(new_i, new_j):
Calculates the g, h, and f values for the new cell.
else:
g_new = self.cell_details[i][j].g + 1.0
h_new = self.calculate_h_value(new_i, new_j)
f_new = g_new + h_new
Updates the cell details if the new f value is better than the current f value and pushes the new cell onto the open_list.
if self.cell_details[new_i][new_j].f == float('inf') or self.cell_details[new_i][new_j].f > f_new:
heapq.heappush(open_list, (f_new, new_i, new_j))
self.cell_details[new_i][new_j].f = f_new
self.cell_details[new_i][new_j].g = g_new
self.cell_details[new_i][new_j].h = h_new
self.cell_details[new_i][new_j].parent_i = i
self.cell_details[new_i][new_j].parent_j = j
End Check:
If the destination is not found after the loop, prints a failure message.
if not found_dest:
print("Failed to find the destination cell")
Please also remember to install the needed libraries! Thanks for reading this short publication, and stay tuned for the next ones, maybe finally the longed-for robot dog...
The research about A* algorithm based on this two sources:
https://www.geeksforgeeks.org/a-search-algorithm/
https://en.wikipedia.org/wiki/A*_search_algorithm
Code:
https://github.com/Marcel3245/A-algorithm-for-leg-simulator
Leave a comment